В этом уроке:
- разбираемся с методами setRectToRect и setPolyToPoly
Матрица позволяет нам не только задавать необходимые преобразования, но и умеет сама их рассчитывать, если мы предоставим ей исходные данные и результат, который мы хотели бы получить.
Рассмотрим пару таких методов.
setRectToRect
Начнем с setRectToRect, который уже как-то помог нам, когда мы изображение с камеры на экран выводили в Уроке 132.
Этот метод берет два прямоугольника и определяет какие преобразования необходимо выполнить над первым прямоугольником, чтобы он полностью поместился во втором. Эти преобразования записываются в матрицу и мы можем ее использовать.
В качестве примера, нарисуем большого снеговика и будем пытаться разместить его в маленьких прямоугольниках.
Создадим проект:
Project name: P1451_MatrixTransform2
Build Target: Android 2.3.3
Application name: MatrixTransform2
Package name: ru.startandroid.develop.p1451matrixtransform2
Create Activity: MainActivity
MainActivity.java:
package ru.startandroid.develop.p1451matrixtransform2;
import android.app.Activity;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Matrix;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.RectF;
import android.os.Bundle;
import android.view.View;
public class MainActivity extends Activity {
@Override
protected void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
setContentView(new DrawView(this));
}
class DrawView extends View {
Paint p;
Path path;
Path pathDst;
RectF rectfBounds;
RectF rectfDst;
Matrix matrix;
public DrawView(Context context) {
super(context);
p = new Paint();
p.setStrokeWidth(3);
p.setStyle(Paint.Style.STROKE);
rectfDst = new RectF();
rectfBounds = new RectF();
path = new Path();
path.addCircle(200, 100, 50, Path.Direction.CW);
path.addCircle(200, 225, 75, Path.Direction.CW);
path.addCircle(200, 400, 100, Path.Direction.CW);
pathDst = new Path();
matrix = new Matrix();
}
@Override
protected void onDraw(Canvas canvas) {
canvas.drawARGB(80, 102, 204, 255);
rectfDst.set(500, 50, 800, 150);
// снеговик
p.setColor(Color.BLUE);
canvas.drawPath(path, p);
// граница снеговика
path.computeBounds(rectfBounds, true);
p.setColor(Color.GREEN);
canvas.drawRect(rectfBounds, p);
// START
// рамка
p.setColor(Color.BLACK);
canvas.drawRect(rectfDst, p);
// преобразование
matrix.reset();
matrix.setRectToRect(rectfBounds, rectfDst, Matrix.ScaleToFit.START);
path.transform(matrix, pathDst);
// снеговик
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
rectfDst.offset(0, 150);
// CENTER
// рамка
p.setColor(Color.BLACK);
canvas.drawRect(rectfDst, p);
// преобразование
matrix.reset();
matrix.setRectToRect(rectfBounds, rectfDst,
Matrix.ScaleToFit.CENTER);
path.transform(matrix, pathDst);
// снеговик
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
rectfDst.offset(0, 150);
// END
// рамка
p.setColor(Color.BLACK);
canvas.drawRect(rectfDst, p);
// преобразование
matrix.reset();
matrix.setRectToRect(rectfBounds, rectfDst, Matrix.ScaleToFit.END);
path.transform(matrix, pathDst);
// снеговик
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
rectfDst.offset(0, 150);
// FILL
// рамка
p.setColor(Color.BLACK);
canvas.drawRect(rectfDst, p);
// преобразование
matrix.reset();
matrix.setRectToRect(rectfBounds, rectfDst, Matrix.ScaleToFit.FILL);
path.transform(matrix, pathDst);
// снеговик
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
}
}
}
Результат:
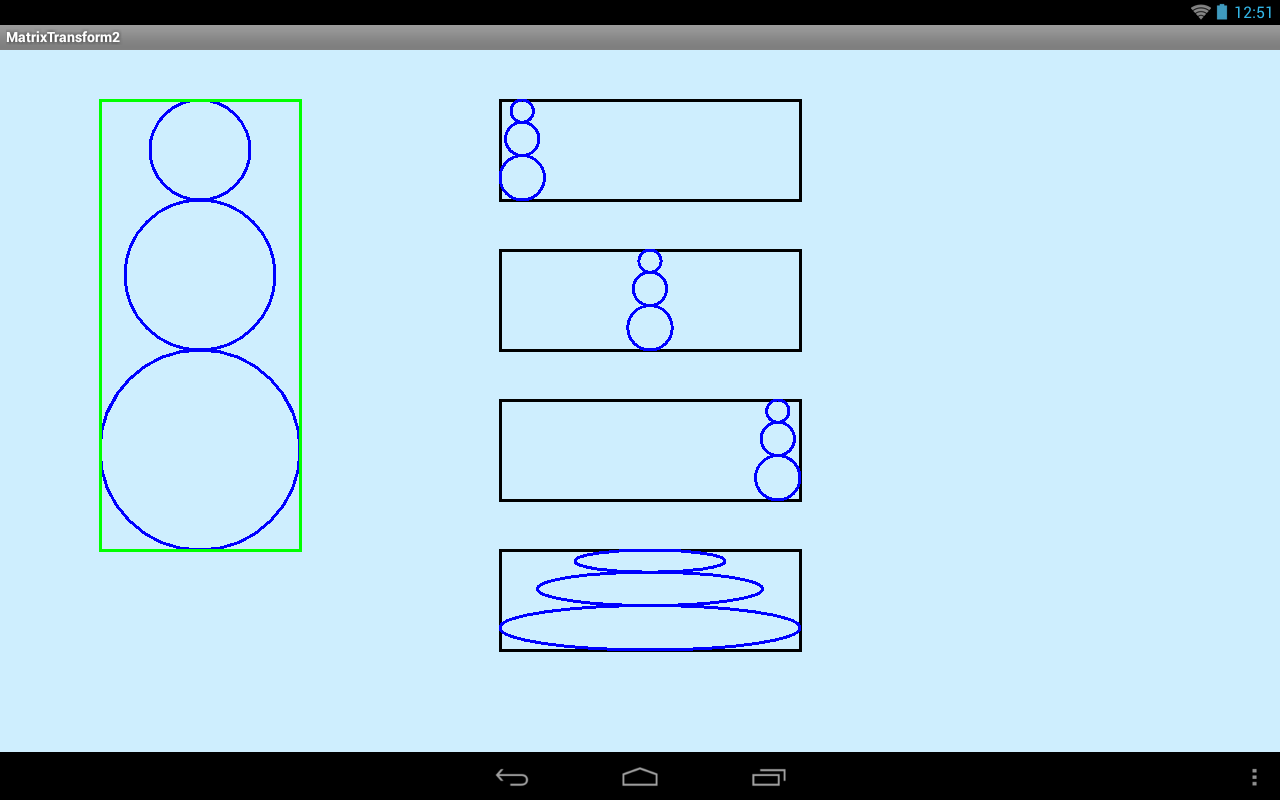
Разбираем код.
Сначала к path добавляем три окружности и получаем снеговика. Рисуем его синим цветом.
Т.к. метод setRectToRect работает с прямоугольниками, нам необходимо получить границы снеговика в виде прямоугольника. Для этого используем метод computeBounds и записываем границы в rectfBounds. Рисуем эти границы зеленым цветом для наглядности.
Далее рисуем первый черный прямоугольник с координатами rectfDst. Методом setRectToRect настраиваем матрицу так, чтобы rectfBounds поместился в rectfDst. При этом необходимо указать ScaleToFit параметр. Мы указываем START. Чуть позже обсудим, что он нам дает. Наша матрица готова и мы используем ее чтобы трансформировать снеговика (path) и выводим результат на экран.
Далее мы три раза повторяем эту же процедуру, смещая координаты черного прямоугольника (rectfDst) вниз на 150 и используя разные ScaleToFit режимы.
Обсудим значение ScaleToFit.
Когда мы один прямоугольник пытаемся вставить в другой, то их соотношения сторон могут не совпадать и первый будет занимать лишь часть внутри второго. Это можно видеть на скриншоте. Если уменьшить снеговика (сохраняя его соотношение сторон), то он занимает лишь часть черного прямоугольника. Параметр ScaleToFit позволяет указать, где разместить снеговика.
START – в левой (или верхней) стороне
CENTER – в центре
END – в правой (или нижней) стороне
FILL – не сохранять соотношение сторон, а растянуть первый прямоугольник так, чтобы он полностью заполнил второй
Именно эти 4 режима в указанном порядке мы и видим на скриншоте.
setPolyToPoly
Метод setPolyToPoly. Крайне нетривиальная для объяснения и понимания штука. Но я вроде нашел способ как наглядно все это изложить. Далее будет очень много букв и постоянные повторения одного и того же разными словами, для лучшего усвоения.
Этот метод, кроме 4-х обычных операций (перемещение, изменение размера, наклон, поворот), позволяет задать в матрице пятую операцию – перспективу. Причем задаем мы их не явно, а указывая исходные и целевые точки. По ним уже матрица сама вычисляет, какие преобразования необходимо сделать.
Точки мы будем задавать через массивы координат. Одна точка – это две координаты. Следовательно, если в массиве, например, 6 координат, то это значит, что в нем 3 точки. Я в тексте буду упоминать и координаты и точки, следите внимательно.
Вкратце опишу основной смысл метода простыми словами. Мы передаем методу два массива координат: исходный и целевой. В исходном массиве содержатся координаты точек до выполнения преобразования. Т.е. как есть сейчас. А в целевом массиве мы задаем координаты, как должно быть после преобразования. И задача метода состоит в настройке матрицы так, чтобы она смогла выполнить такое преобразование: т.е. получить целевые точки из исходных.
Одна точка
Простой пример с одной точкой. В метод setPolyToPoly мы передаем исходный массив координат {100,100} и целевой массив координат {150,120}. Метод setPolyToPoly должен настроить матрицу так, чтобы после выполнения преобразования у нас то, что находится в точке (100,100) оказалось бы в точке (150,120). Т.е. в этом случае – это просто смещение на 50 вправо и на 20 вниз.
Давайте посмотрим, как накодить такой пример.
Перепишем класс DrawView:
class DrawView extends View {
Paint p;
Path path;
Path pathDst;
RectF rectf;
Matrix matrix;
float[] src;
float[] dst;
public DrawView(Context context) {
super(context);
p = new Paint();
p.setStrokeWidth(3);
p.setStyle(Paint.Style.STROKE);
path = new Path();
pathDst = new Path();
matrix = new Matrix();
rectf = new RectF(100, 100, 200, 200);
src = new float[] { 100, 100 };
dst = new float[] { 150, 120 };
}
@Override
protected void onDraw(Canvas canvas) {
canvas.drawARGB(80, 102, 204, 255);
// зеленый квадрат
path.reset();
path.addRect(rectf, Path.Direction.CW);
p.setColor(Color.GREEN);
canvas.drawPath(path, p);
// преобразование
matrix.setPolyToPoly(src, 0, dst, 0, 1);
path.transform(matrix, pathDst);
// синий квадрат
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
}
}
В path добавляем квадрат и рисуем его на экране зеленым цветом.
Далее используем метод setPolyToPoly. Он принимает 5 параметров:
- массив исходных координат
- позиция элемента в массиве исходных координат, с которого начинаем формировать точки
- массив целевых координат
- позиция элемента в массиве целевых координат, с которого начинаем формировать точки
- кол-во точек, которые метод setPolyToPoly возьмет из массивов и использует для настройки матрицы
В качестве массива исходных координат мы передаем массив из двух чисел 100 и 100. Они являются координатами одной исходной точки (100,100).
В качестве массива целевых координат мы передаем массив из двух чисел 150 и 120. Они являются координатами одной целевой точки (150,120).
Позиции элементов в массиве будем всегда указывать 0, т.е. начинаем формировать точки с первого элемента.
Кол-во точек указываем 1. Т.к. два элемента массива – это две координаты – это одна точка.
Матрица настроена, применяем ее к path и рисуем результат синим цветом.
Теперь разберемся, какой смысл несут исходная и целевая точки. Когда мы используем всего по одной исходной и целевой точке, матрица настраивает трансформацию перемещения. Говоря простыми словами, матрица настроится так, чтобы исходная точка (100,100) после преобразования находилась в целевой точке (150,120).
Взглянем на результат, чтобы лучше понять
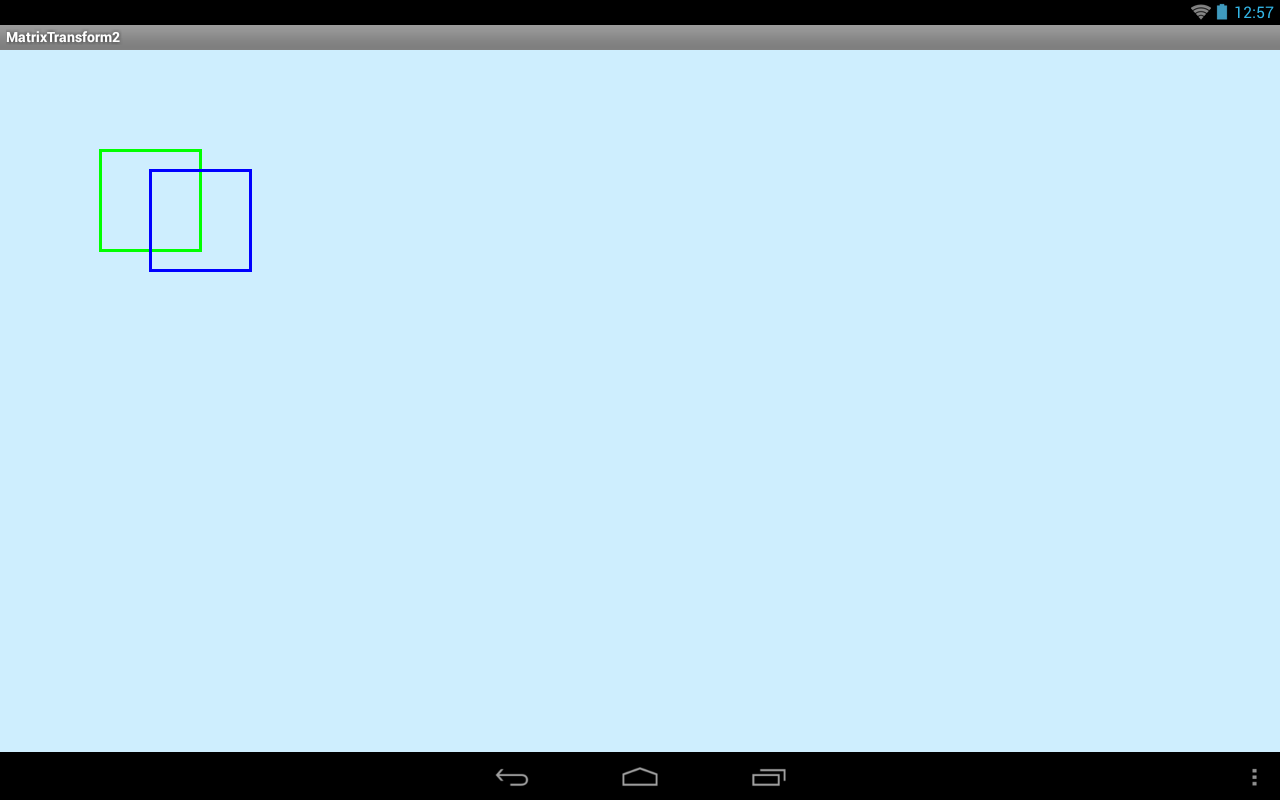
У зеленого квадрата верхний левый угол – это точка (100,100), это мы задавали в rectf. Матрицу мы настроили так, чтобы то, что было в точке (100,100) после преобразования оказалось бы в точке (150,120). А следовательно, т.к. в точке (100,100) у нас был левый верхний угол квадрата, то после преобразования этот угол переехал в точку (150,120), что и отражает синий квадрат (pathDst). Разумеется, преобразование применилось не к одной точке, а ко всей фигуре: она вся сместилась. Но для настройки этого преобразования достаточно одной точки.
Т.е. таким нетривиальным способом мы просто выполнили перемещение. Сделали мы это просто указав, что после преобразования то, что было в исходной точке, должно находится в целевой точке. В нашем случае это был верхний левый угол квадрата. Причем, необязательно указывать именно точку квадрата. С тем же успехом мы могли бы указать любую другую точку квадрата или вообще точку вне квадрата. Матрица все равно настроила бы перемещение (если конечно исходная и целевая точки различны) и квадрат бы переместился после выполнения преобразования. Просто, используя точку квадрата получается понятнее и нагляднее.
Это мы рассмотрели метод setPolyToPoly на примере указания одной точки (одной исходной и одной целевой). И увидели, что одна точка задает перемещение. А таких точек мы можем указать от одной до четырех.
Две точки
Давайте посмотрим, что нам даст использование двух точек.
Перепишем класс DrawView:
class DrawView extends View {
Paint p;
Paint pBlack;
Path path;
Path pathDst;
RectF rectf;
Matrix matrix;
float[] src;
float[] dst;
float[] dst2;
int points = 1;
public DrawView(Context context) {
super(context);
p = new Paint();
p.setStrokeWidth(3);
p.setStyle(Paint.Style.STROKE);
pBlack = new Paint();
pBlack.setColor(Color.BLACK);
pBlack.setStrokeWidth(3);
path = new Path();
pathDst = new Path();
matrix = new Matrix();
rectf = new RectF(100,100,200,200);
src = new float[]{100,100,200,200};
dst = new float[]{50,300,250,500};
dst2 = new float[]{400,200,500,200};
}
@Override
protected void onDraw(Canvas canvas) {
canvas.drawARGB(80, 102, 204, 255);
// зеленый квадрат
path.reset();
path.addRect(rectf, Path.Direction.CW);
p.setColor(Color.GREEN);
canvas.drawPath(path, p);
canvas.drawLine(src[0], src[1], src[2], src[3], pBlack);
// синий квадрат
// преобразование
matrix.setPolyToPoly(src, 0, dst, 0, points);
path.transform(matrix, pathDst);
// рисование
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
canvas.drawLine(dst[0], dst[1], dst[2], dst[3], pBlack);
// красный квадрат
// преобразование
matrix.setPolyToPoly(src, 0, dst2, 0, points);
path.transform(matrix, pathDst);
// рисование
p.setColor(Color.RED);
canvas.drawPath(pathDst, p);
canvas.drawLine(dst2[0], dst2[1], dst2[2], dst2[3], pBlack);
}
}
Результат:
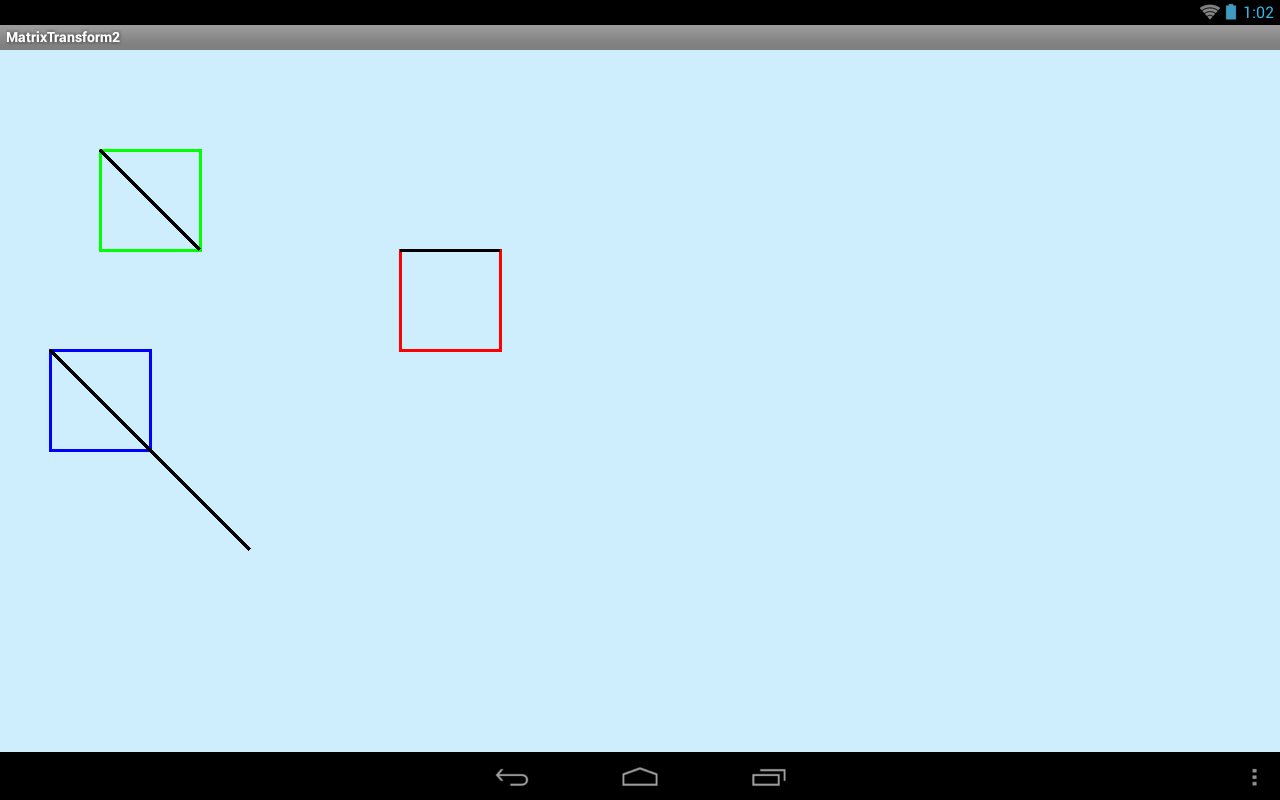
У нас есть три массива: src – исходные координаты, и два массива целевых координат dst и dst2. В каждом массиве по 4 элемента. Т.к. 4 координаты = 2 точки, то у нас пара исходных точек и две пары целевых точек. Две пары целевых нужны, чтобы показать два примера преобразования. Т.е. будем две матрицы настраивать.
Используем все тот же квадрат rectf. Добавляем его в path и выводим на экран зеленым цветом. Тут же черным цветом рисуем линию, заданную парой исходных точек. Это нам необходимо для наглядности. К матрице эта линия не имеет никакого отношения. Она просто поможет лучше увидеть и понять механизм. Исходные точки мы задали так, что эта линия является диагональю квадрата. Это видно на скриншоте, у зеленого квадрата.
Далее выполняем настройку матрицы методом setPolyToPoly. Отдаем исходный массив(src) и первый целевой(dst). Тут обратите внимание на то, что массивы содержат по 4 координаты, а значит по 2 точки. А переменная points, которую мы передаем в setPolyToPoly, равна 1. Т.е. мы говорим методу, чтобы он для настройки матрицы использовал только одну точку (первые два элемента) из каждого массива, а вторые точки пока проигнорировал.
Тем самым мы снова, как и в прошлом примере, используем одну точку. А значит, получим просто перемещение. В нашем случае это перемещение из точки (100,100) (первые два элемента массива src) в точку (50,300) (первые два элемента массива dst).
После настройки матрицы синим цветом выводим результат преобразования. На скриншоте видно, что левый верхний угол синего квадрата находится в точке (50,300) из dst, как мы и заказывали. Тут же нарисуем черную линию, заданную парой целевых точек из dst. Чуть позже разберемся, зачем это нужно.
Далее мы аналогично выполняем преобразование используя тот же исходный массив (src) и второй целевой (dst2). И выводим результат красным цветом. Левый верхний угол находится в (400,200) из dst2. На скриншоте это видно. И снова рисуем черную линию, заданную парой целевых точек из dst2.
Итак, по сравнению с прошлым примером, здесь мы брали массивы с двумя точками (4 координаты), а не одной точкой (2 координаты). Но при этом в методе setPolyToPoly пока что указали, что использовать надо только одну точку. Т.е. матрица нам просто настроила перемещение, что мы и увидели на экране.
Зачем тогда нужны вторые точки? Пока что мы их использовали только для рисования черных линий – между первой и второй точками. Вот об этих линиях мы сейчас и поговорим.
Вспоминаем логику одной точки. То, что было в исходной точке, должно после преобразования оказаться в целевой точке. Аналогично сформулируем логику для двух точек. То, что находится на линии, заданной двумя исходными точками, после преобразования должно оказаться на линии, заданной двумя целевыми точками. Соответственно, мы даем методу setPolyToPoly две этих линии: исходную(массив src) и целевую(массив dst), и он по ним настраивает матрицу.
Снова смотрим на скрин

Зеленый квадрат у нас исходный, а синий и красный – целевые.
Черными цветом мы нарисовали нужные нам линии. У зеленого квадрата эта линия из исходного массива src: (100,100)-(200,200). У синего – из целевого dst (50,300)-(250,500). Значит, после преобразования то, что было на линии (100,100)-(200,200) должно оказаться на линии (50,300)-(250,500). А т.к. на линии (100,100)-(200,200) у нас находится диагональ исходного квадрата, значит диагональ целевого квадрата должна оказаться линией (50,300)-(250,500). Т.е. синий квадрат должен увеличиться в размере так, чтобы его диагональ совпала с его черной линией.
Пока что это не произошло потому, что мы методу setPolyToPoly передали указание использовать только одну точку. Вторую он не учитывает при расчетах преобразований.
С красным квадратом все аналогично. Его диагональ должна быть там, где проходит его черная линия. Получается, что для этого ему придется немного повернуться против часовой и уменьшится в размере.
Давайте в нашем коде включим использование вторых точек и посмотрим на результат преобразований. Переменной points присвойте значение 2 вместо 1.
int points = 2;
Результат:
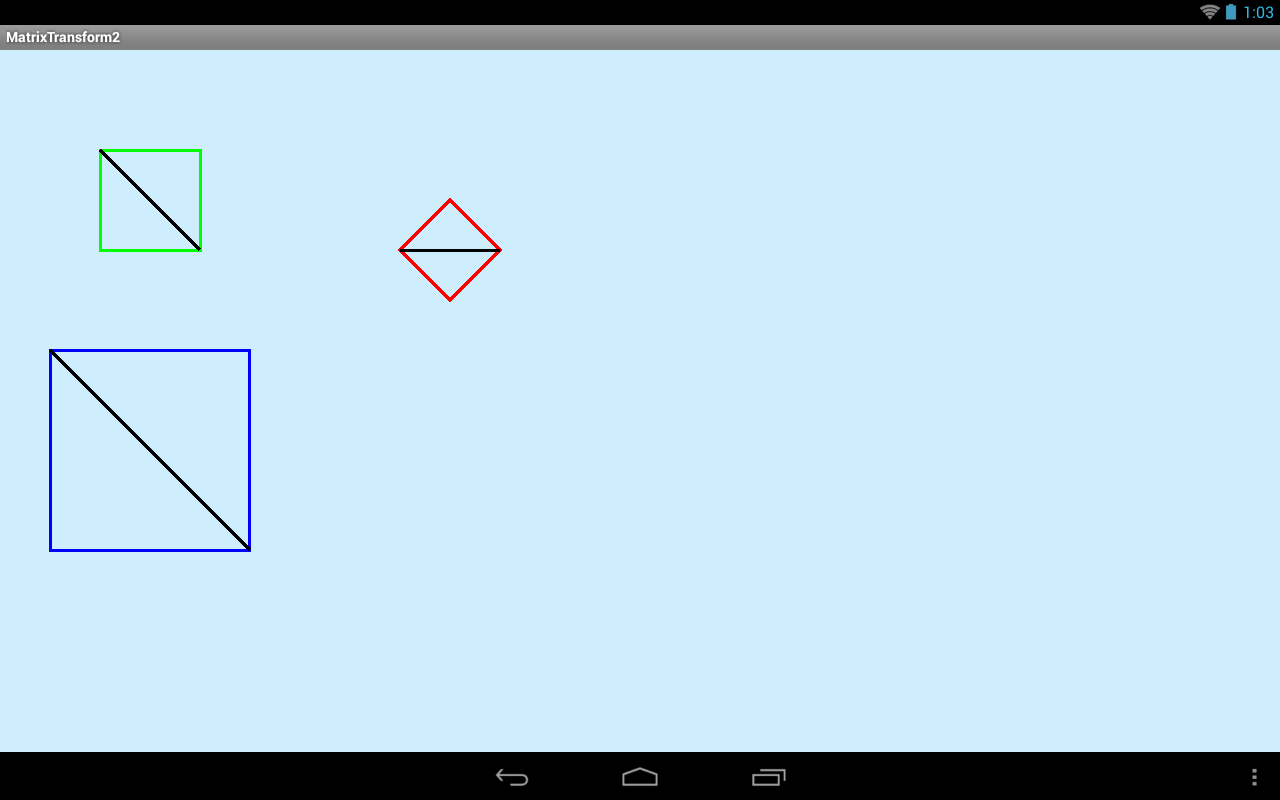
Все как мы и просили. Диагонали целевых квадратов полностью заняли черные линии. Т.е. мы, тем самым, в матрицах задали не только перемещение, но и изменение размера и поворот, используя по две точки.
Подытожим.
Одна точка (массив из двух координат) позволила нам задать перемещение.
Две точки (массив из четырех координат) позволили нам задать перемещение, поворот и изменение размера.
Три точки
Смотрим пример с тремя точками.
Перепишем класс DrawView:
class DrawView extends View {
Paint p;
Paint pBlack;
Paint pGray;
Path path;
Path pathDst;
RectF rectf;
Matrix matrix;
float[] src;
float[] dst;
float[] dst2;
int points = 2;
public DrawView(Context context) {
super(context);
p = new Paint();
p.setStrokeWidth(3);
p.setStyle(Paint.Style.STROKE);
pGray = new Paint();
pGray.setColor(Color.GRAY);
pGray.setStrokeWidth(3);
pBlack = new Paint();
pBlack.setColor(Color.BLACK);
pBlack.setStrokeWidth(3);
path = new Path();
pathDst = new Path();
matrix = new Matrix();
rectf = new RectF(100,100,200,200);
src = new float[]{100,100,200,200,200,100};
dst = new float[]{50,300,250,500,230,350};
dst2 = new float[]{400,200,500,200,440,100};
}
@Override
protected void onDraw(Canvas canvas) {
canvas.drawARGB(80, 102, 204, 255);
// зеленый квадрат
path.reset();
path.addRect(rectf, Path.Direction.CW);
p.setColor(Color.GREEN);
canvas.drawPath(path, p);
canvas.drawLine(src[0], src[1], src[2], src[3], pBlack);
canvas.drawLine(src[0], src[1], src[4], src[5], pGray);
// синий квадрат
// преобразование
matrix.setPolyToPoly(src, 0, dst, 0, points);
path.transform(matrix, pathDst);
// рисование
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
canvas.drawLine(dst[0], dst[1], dst[2], dst[3], pBlack);
canvas.drawLine(dst[0], dst[1], dst[4], dst[5], pGray);
// красный квадрат
// преобразование
matrix.setPolyToPoly(src, 0, dst2, 0, points);
path.transform(matrix, pathDst);
// рисование
p.setColor(Color.RED);
canvas.drawPath(pathDst, p);
canvas.drawLine(dst2[0], dst2[1], dst2[2], dst2[3], pBlack);
canvas.drawLine(dst2[0], dst2[1], dst2[4], dst2[5], pGray);
}
}
Код похож на предыдущий пример. Но теперь в массивы мы добавили еще по одной точке (по две координаты). Теперь массивы состоят из 6-ти элементов-координат, а значит из них можно составить по три точки.
Что делают первые две мы уже знаем. Разберемся что нам даст третья.
Для этого мы снова рисуем линии заданные первой и третьей точкой массива. Нарисуем их серым цветом (pGray). А параметр points для метода setPolyToPoly укажем пока равным двум. Т.е. метод пока будет рассчитывать матрицу исходя из двух точек, а третьи проигнорит.
Посмотрим результат
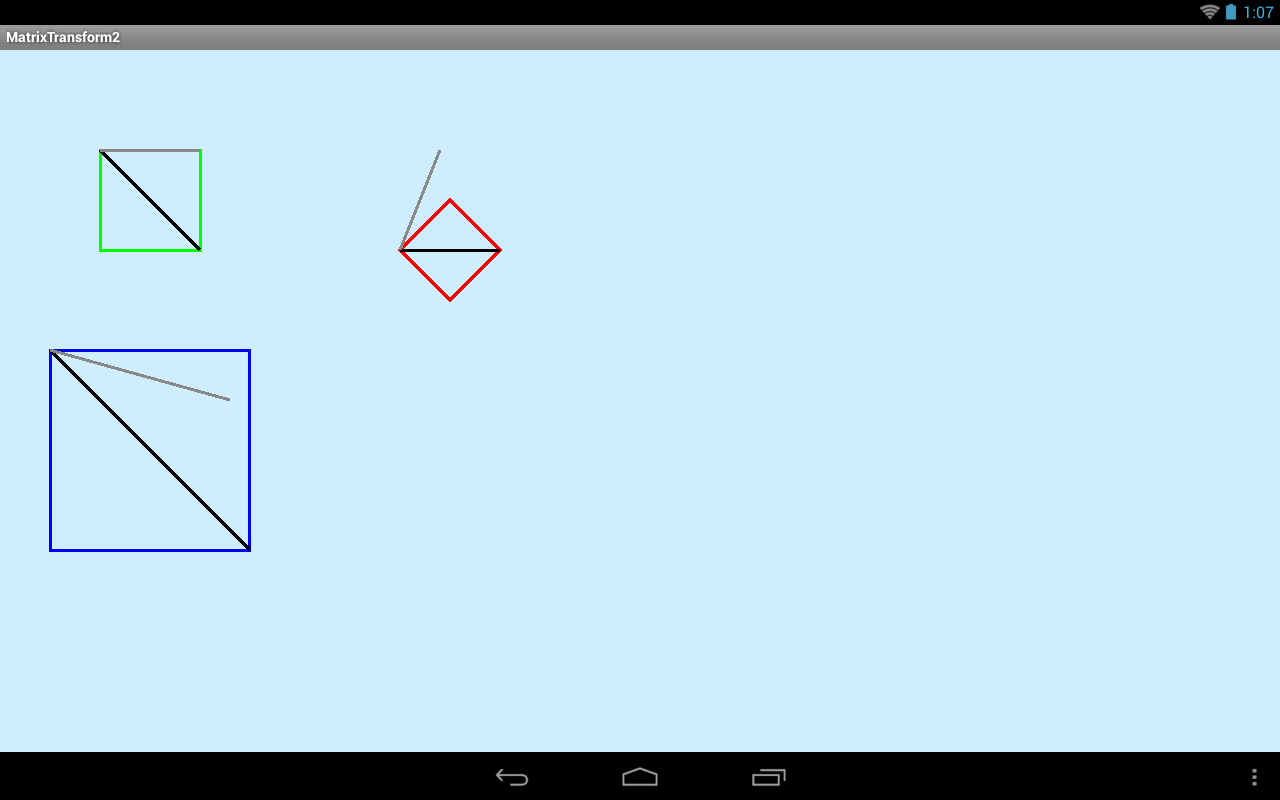
Почти та же картинка, что и в прошлом примере. Используя первые две точки из массивов матрица настроила преобразование зеленого квадрата в синий и красный.
Но теперь на рисунке видны серые линии. Напомню, что это линия задана первой и третьей (новой) точкой из массива. Смысл тут тот же: то, что находится на исходной линии, должно оказаться на целевой. Но в случае с третьей точкой это позволяет задать нам наклон (skew) квадрата.
У зеленого (исходного) квадрата серая линия является его верхней гранью. А значит, синий и красной массивы должны быть нарисованы так, чтобы их верхние грани легли на их серые линии. А т.к. мы используем для этого третью точку, то это должно быть сделано с помощью наклона, а не перемещения или поворота (их мы задавали второй точкой).
Давайте включим использование методом setPolyToPoly всех трех точек, поменяв в коде значение параметра points на 3:
int points = 3;
Результат
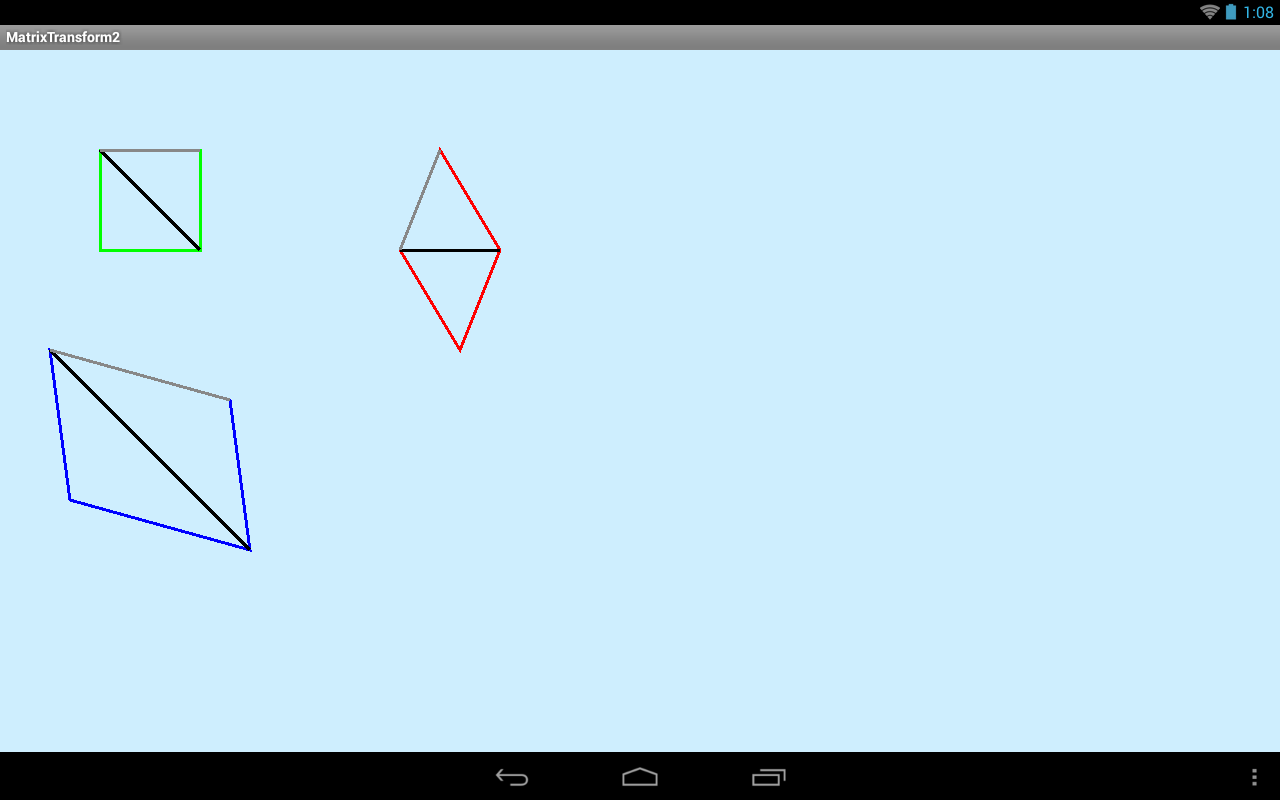
Квадраты наклонились так, чтобы их верхние грани совпали с серыми линиями. Т.е. тем самым мы задали наклон.
Снова подытожим.
Одна точка (массив из двух координат) позволила нам задать перемещение.
Две точки (массив из четырех координат) позволили нам задать перемещение, поворот и изменение размера.
Три точки (массив из шести координат) позволили нам задать перемещение, поворот, изменение размера и наклон.
Очень надеюсь, что вам постепенно раскрывается смысл всего этого механизма)
Четыре точки
Остается 4-я точка.
Перепишем класс DrawView:
class DrawView extends View {
Paint p;
Paint pBlack;
Paint pGray;
Paint pWhite;
Path path;
Path pathDst;
RectF rectf;
Matrix matrix;
float[] src;
float[] dst;
float[] dst2;
int points = 3;
public DrawView(Context context) {
super(context);
p = new Paint();
p.setStrokeWidth(3);
p.setStyle(Paint.Style.STROKE);
pGray = new Paint();
pGray.setColor(Color.GRAY);
pGray.setStrokeWidth(3);
pBlack = new Paint();
pBlack.setColor(Color.BLACK);
pBlack.setStrokeWidth(3);
pWhite = new Paint();
pWhite.setColor(Color.WHITE);
pWhite.setStrokeWidth(3);
path = new Path();
pathDst = new Path();
matrix = new Matrix();
rectf = new RectF(100,100,200,200);
src = new float[]{100,100,200,200,200,100,100,200};
dst = new float[]{50,300,250,500,230,350,40,550};
dst2 = new float[]{400,200,500,200,440,100,440,230};
}
@Override
protected void onDraw(Canvas canvas) {
canvas.drawARGB(80, 102, 204, 255);
// зеленый квадрат
path.reset();
path.addRect(rectf, Path.Direction.CW);
p.setColor(Color.GREEN);
canvas.drawPath(path, p);
canvas.drawLine(src[0], src[1], src[2], src[3], pBlack);
canvas.drawLine(src[0], src[1], src[4], src[5], pGray);
canvas.drawLine(src[0], src[1], src[6], src[7], pWhite);
// синий квадрат
// преобразование
matrix.setPolyToPoly(src, 0, dst, 0, points);
path.transform(matrix, pathDst);
// рисование
p.setColor(Color.BLUE);
canvas.drawPath(pathDst, p);
canvas.drawLine(dst[0], dst[1], dst[2], dst[3], pBlack);
canvas.drawLine(dst[0], dst[1], dst[4], dst[5], pGray);
canvas.drawLine(dst[0], dst[1], dst[6], dst[7], pWhite);
// красный квадрат
// преобразование
matrix.setPolyToPoly(src, 0, dst2, 0, points);
path.transform(matrix, pathDst);
// рисование
p.setColor(Color.RED);
canvas.drawPath(pathDst, p);
canvas.drawLine(dst2[0], dst2[1], dst2[2], dst2[3], pBlack);
canvas.drawLine(dst2[0], dst2[1], dst2[4], dst2[5], pGray);
canvas.drawLine(dst2[0], dst2[1], dst2[6], dst2[7], pWhite);
}
}
Код похож на прошлый пример с тремя точками. Теперь мы добавили еще по паре координат в массивы, чтобы получить четвертые точки. И для каждого квадрата нарисовали белые линии заданные первой и четвертой точками.
Параметр points для метода setPolyToPoly укажем пока равным 3. Т.е. метод пока будет рассчитывать матрицу исходя из трех точек, а четвертые проигнорит.
Результат:
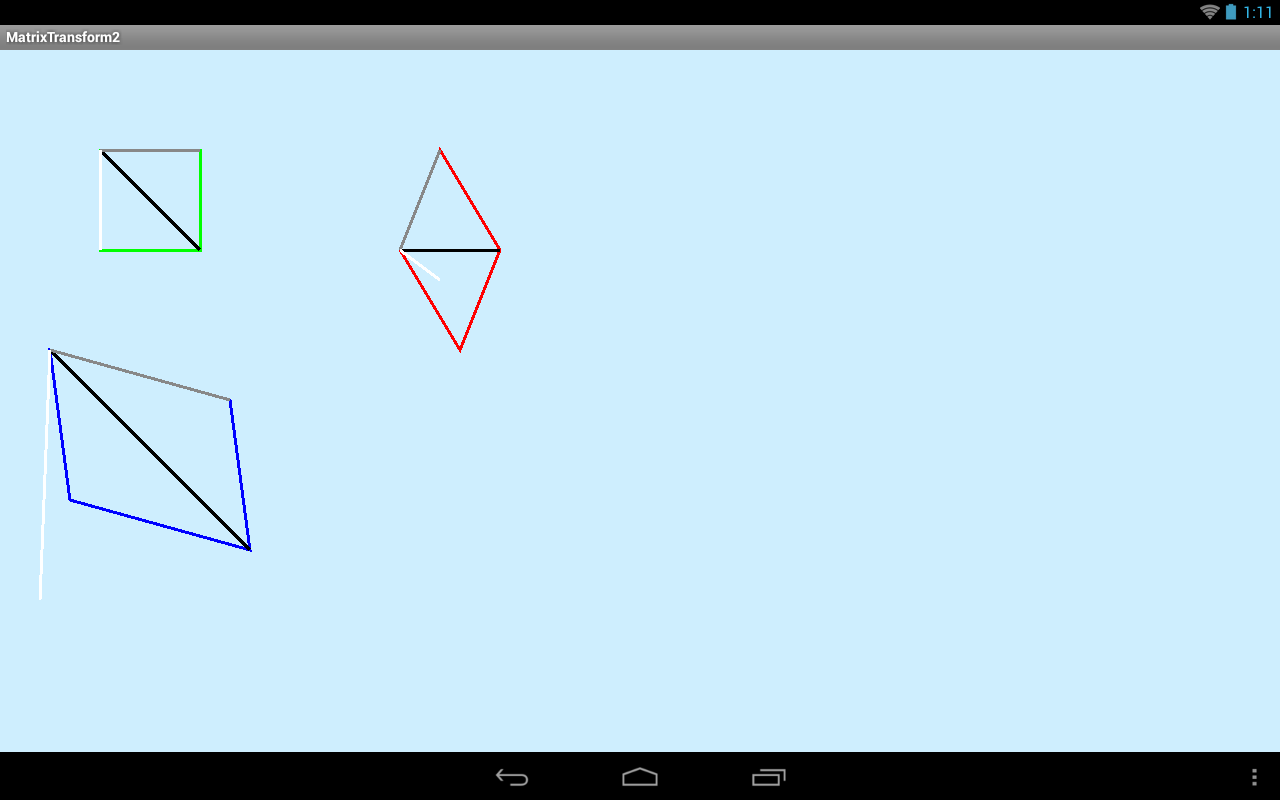
Почти та же картинка, что и в прошлый раз. Матрица по трем точкам рассчитала перемещение, поворот, изменение размера и наклон и мы видим результаты преобразования: синий и красный квадраты.
Белые линии квадратов заданы первой и четвертой точками. Смысл снова тот же: то, что находится на исходной линии, должно оказаться на целевой. В случае с четвертой точкой это позволяет задать нам что-то типа перспективы для квадрата.
У зеленого (исходного) квадрата белая линия является его левой гранью. А значит, синий и красной массивы должны быть нарисованы так, чтобы их левые грани легли на их белые линии. А т.к. мы используем для этого четвертую точку, то это должно быть сделано с помощью перспективы, а не наклона (третья точка) или перемещения и поворота (их мы задавали второй точкой).
Давайте включим использование методом setPolyToPoly всех четырех точек, поменяв в коде значение параметра points на 4:
int points = 4;
Результат:
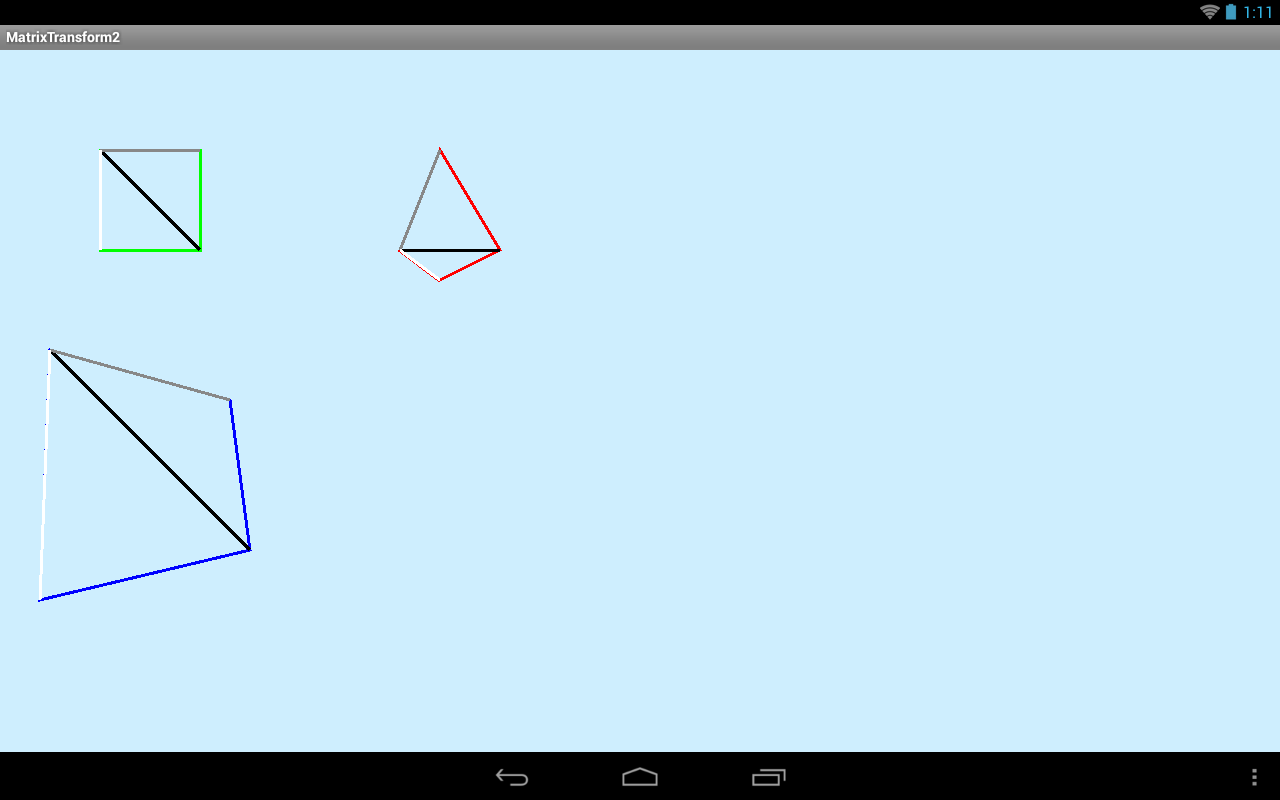
Квадраты деформировались так, чтобы их левые грани совпали с белыми линиями. Результат выглядит как перспектива.
Подытожим.
Одна точка (массив из двух координат) позволила нам задать перемещение.
Две точки (массив из четырех координат) позволили нам задать перемещение, поворот и изменение размера.
Три точки (массив из шести координат) позволили нам задать перемещение, поворот, изменение размера и наклон.
Четыре точки (массив из восьми координат) позволили нам задать перемещение, поворот, изменение размера, наклон и перспективу.
В общем, объяснил, как смог. Понятнее уже точно не смогу) Советую вам посдвигать немного точки в массивах и понаблюдать за результатами. Для этого можно использовать сразу последний пример. А значением points вы можете регулировать кол-во используемых точек: от 1 до 4.
Метод setPolyToPoly кроме настройки матрицы возвращает нам boolean значение. Этим он сообщает: получилось у него настроить матрицу или требования были противоречивы и настройка невозможна.
В процессе создания урока вспомнилась книга Флатландия. Если еще не читали, то рекомендую, весьма занятное произведение.
На следующем уроке:
- используем матрицу канвы для преобразований
Присоединяйтесь к нам в Telegram:
- в канале StartAndroid публикуются ссылки на новые статьи с сайта startandroid.ru и интересные материалы с хабра, medium.com и т.п.
- в чатах решаем возникающие вопросы и проблемы по различным темам: Android, Compose, Kotlin, RxJava, Dagger, Тестирование, Performance
- ну и если просто хочется поговорить с коллегами по разработке, то есть чат Флудильня




